Τελ. ενημέρωση:
   19-Sep-2000
 

Αρχ Ελλ Ιατρ, 16(5), Σεπτέμβριος-Οκτώβριος 1999, 430-432

ΑΡΘΡO ΣΥΝΤΑΞΗΣ

Διάστημα ασφαλείας των διαγνωστικών δοκιμασιών

Λ. ΣΠΑΡΟΣ
Εργαστήριο Κλινικής Επιδημιολογίας, Τμήμα Νοσηλευτικής, Πανεπιστήμιο Αθηνών

Η διάγνωση, ως γνωστό, δεν είναι αυτοσκοπός, αλλά εξυπηρετεί πρακτικές επιδιώξεις, κυρίως θε ρα πευτικές ή και απλώς προγνωστικές.1 Η διάγνωση, ως διαδικασία, υπακούει στο λογικό σχήμα της στατιστικής (ή στοχαστικής ή πιθανολογικής) εξήγησης.2 Η διαγνωστική έρευνα επιδιώκει να διαμορφώσει μια γενική πρόταση ή, με άλλη διατύπωση, ένα νόμο, στον οποίο να ανάγεται κάθε συγκεκριμένη περίπτωση αρρώστιας. Η πλέον γνωστή μέθοδος διαγνωστικής έρευνας είναι η μπαγιεσιανή, ενώ η μέθοδος της λογιστικής παλινδρόμησης δεν έχει τύχει ακόμη της ανάλογης ερευνητικής προσοχής.3 Παρά την έντονη κριτική που έχει ασκηθεί στην μπαγιεσιανή προσέγγιση, αυτή εξακολουθεί να αποτελεί τη μόνη μέθοδο που χρησιμοποιείται από την ακαδημαϊκή Ιατρική.4 Η βάση της λογικής αυτή προσέγγισης είναι ότι η διαγνωστική πιθανότητα ενός νοσήματος (Ν), δηλαδή η πιθανότητα ενός συγκεκριμένου νοσήματος με δεδομένη μια κλινική εικόνα ή το αποτέλεσμα μίας ή περισσοτέρων εργαστηριακών δοκιμασιών, είναι συνάρτηση αφενός της συχνότητας, δηλαδή του επιπολασμού του Ν, και αφετέρου της κλινικής εικόνας με δεδομένο το αναζητούμενο Ν και των διαφοροδιαγνωστικών συναφών νοσημάτων. Ο επιπολασμός του νοσήματος, που καθορίζεται από στοιχεία που δεν περιλαμβάνονται στην κλινική εικόνα αλλά αποτελούν το προφίλ κινδύνου, όπως επικράτησε να λέγεται σήμερα, όπως είναι η ηλικία, το φύλο, ο χώρος εργασίας κ.ά., φέρεται και ως πρωτογενής ή εκ των προτέρων ή προ της δοκιμασίας πιθανότητα.

Η συχνότητα της κλινικής εικόνας ή του θετικού αποτελέσματος μιας δοκιμασίας στο νόσημα που αναζητείται (Ν) φέρεται ως ποσοστό αληθώς θετικών αποτελεσμάτων ή ως πιθανοφάνεια των αληθώς θετικών ευρημάτων, ενώ το αντίστοιχο ποσοστό στα διαφοροδιαγνωστικώς συναφή νοσήματα Ν ως ποσοστό (ή πιθανοφάνεια) των ψευδώς θετικών ευρημάτων. Ο λόγος των δύο αυτών ποσοστών (ή πιθανοφανειών) φέρεται ως θετικός λόγος πιθανοφάνειας και συμβολίζεται με το γράμμα L. Αντίθετα, ο λόγος του ποσοστού των ψευδώς αρνητικών προς το ποσοστό των αληθώς αρνητικών ευρημάτων φέρεται ως αρνητικός λόγος πιθανοφάνειας και συμβολίζεται με το γράμμα λ.

Τέλος, η πιθανότητα του νοσήματος Ν με δεδομένη την κλινική εικόνα ή το θετικό αποτέλεσμα της δοκιμασίας φέρεται ως θετική διαγνωστική πιθανότητα ή αξία ή εκ των υστέρων πιθανότητα ή δευτερογενής πιθανότητα.5–7 Η ύπαρξη των πολλών συνωνύμων, για ν' αποδοθούν οι απλές αυτές έννοιες, αποτελεί έναν από τους σημαντικούς λόγους που έχουν δυσχεράνει την κατανόηση του λογικού σχήματος της μπαγιεσιανής διαγνωστικής εξήγησης.

Με βάση τα παραπάνω σύμβολα, η δευτερογενής πιθανότητα (ΔΠ) υπολογίζεται από τους παρακάτω τύπους:8

α. Όταν το αποτέλεσμα μιας δοκιμασίας είναι θετικό, η ΔΠ (ΘΔΠ) υπολογίζεται από τον τύπο:

όπου p=πρωτογενής πιθανότητα (ή ο επιπολασμός) του Ν.

β. Όταν το αποτέλεσμα της δοκιμασίας είναι αρνητικό, η ΔΠ (ΑΔΠ) υπολογίζεται από τον τύπο:

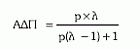
Όπως προκύπτει από τη διερεύνηση των δύο αυτών τύπων, όταν η πρωτογενής πιθανότητα του Ν αυξάνει, η ΘΔΠ αυξάνει και η ΑΔΠ ελαττώνεται και, αντίθετα, όταν η πρωτογενής πιθανότητα του Ν ελαττώνεται, η ΘΔΠ ελαττώνεται και η ΑΔΠ αυξάνει.

Η κοινωνική απαίτηση περιορισμού του κόστους, με την ευρεία έννοια του όρου, επέβαλε την καλύτερη κατανόηση της πληροφορίας που παρέχει μια εργαστηριακή δοκιμασία σε συνάρτηση με την, προ της εφαρμογής της, πιθανότητα του νοσήματος Ν. Για το σκοπό αυτόν, είναι ιδιαίτερα χρήσιμη η έννοια του διαστήματος ασφαλείας.8

Διάστημα ασφαλείας

Στην εικόνα 1 φαίνεται η γραφική παράσταση της σχέσης που συνδέει την πρωτογενή με τη δευτερογενή διαγνωστική πιθανότητα. Η καμπύλη πάνω από τη διαγώνιο εκφράζει τις δευτερογενείς πιθανότητες όταν το αποτέλεσμα της δοκιμασίας είναι θετικό (ΘΔΠ), ενώ η καμπύλη κάτω από τη διαγώνιο εκφράζει τη δευτερογενή πιθανότητα όταν η δοκιμασία είναι αρνητική. Η πιθανότητα αυτή φέρεται και ως αρνητικό προβλεπτικό σφάλμα (nega tive predictive error). Η οριζόντια γραμμή παριστάνει δευτερογενή πιθανότητα ίση προς 0,50 και αποτελεί την απλούστερη μορφή του ουδού απόφασης.

Οι δύο πρωτογενείς πιθανότητες p1 και p2 ορίζουν τρία διαστήματα: (α) το διάστημα 0 έως p1, (β) το διάστημα p1 έως p2 ή διάστημα ασφαλείας και (γ) το διάστημα p2 έως 1. Όταν η πρωτογενής διαγνωστική πιθανότητα περιλαμβάνεται στο διάστημα 0 έως p1, η δευτερογενής (μετά το αποτέλεσμα της δοκιμασίας Τ) πιθανότητα παραμένει μικρότερη του 0,50, είτε το αποτέλεσμα της δοκιμασίας είναι θετικό είτε αρνητικό. Όταν η πρωτογενής πιθανότητα περιλαμβάνεται στο τρίτο διάστημα (p2 έως 1), η δευτερογενής πιθανότητα είναι μεγαλύτερη του 0,50, είτε το αποτέλεσμα της δοκιμασίας (Τ) είναι θετικό είτε αρνητικό. Στις δύο αυτές περιπτώσεις, η παραγγελία της δοκιμασίας είναι διαγνωστικά περιττή.

Όταν, αντίθετα, η πρωτογενής πιθανότητα περιλαμβάνεται μεταξύ των p1 και p2, τότε το μεν θετικό αποτέλεσμα της δοκιμασίας δίνει θετική δευτερογενή διαγνωστική πιθανότητα μεγαλύτερη από 0,50, ενώ το αρνητικό αποτέλεσμα δίνει δευτερογενή πιθανότητα ή αρνητικό διαγνωστικό σφάλμα μικρότερο του 0,50. Το διάστημα αυτό φέρεται ως διάστημα ασφαλείας (security interval) της δοκιμασίας, γιατί σ' αυτό το διάστημα το θετικό αποτέλεσμα δίνει μεγαλύτερη πιθανότητα στην παρουσία του Ν παρά στην απουσία του, ενώ το αντίθετο ισχύει όταν το αποτέλεσμα είναι αρνητικό.

Οι δύο πρωτογενείς πιθανότητες του Ν (p1 και p2) υπολογίζονται με τους παρακάτω τύπους:

Παράδειγμα

Εάν ο θετικός λόγος πιθανοφάνειας (L) μιας δοκιμασίας Τ ισούται με L=3 και ο αρνητικός με λ=0,50, τότε οι πρωτογενείς πιθανότητες p1 και p2 ισούνται με:

Το διάστημα ασφαλείας της δοκιμασίας περιλαμβάνεται μεταξύ των τιμών 0,25 και 0,67. Όταν, δηλαδή, η πρωτογενής πιθανότητα (ο επιπολασμός) του νοσήματος είναι μικρότερη του 0,25 ή μεγαλύτερη του 0,67, τότε το θετικό ή αρνητικό αποτέλεσμα της δοκιμασίας δεν συμβάλλει διαγνωστικά. Όταν η πρωτογενής πιθανότητα του Ν είναι 0,45, τότε η θετική (δευτερογενής) διαγνωστική πιθανότητα (η αξία) ισούται με την αρνητική* (δευτερογενή) διαγνωστική πιθανότητα (ή αξία) και υπολογίζεται από τον τύπο:

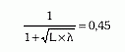
Όταν η πρωτογενής πιθανότητα έχει την τιμή αυτή, τότε το διαγνωστικό κέρδος, δηλαδή η απόσταση της δευτερογενούς (ΘΔΠ=0,71) από την πρωτογενή πιθανότητα (=0,45), λαμβάνει τη μέγιστη τιμή της (0,71–0,45=0,26).

Η κατανόηση του διαστήματος ασφαλείας μιας δοκιμασίας θα βοηθήσει ν' αποφευχθούν αρκετά σφάλματα ερμηνείας των αποτελεσμάτων των εργαστηριακών δοκιμασιών, των οποίων οι συνέπειες στη λήψη των διαγνωστικών αλλά και θεραπευτικών αποφάσεων είναι σημαντικές για τον άρρωστο.

 


*Η αρνητική διαγνωστική πιθανότητα (αξία) είναι η πιθανότητα να μην πάσχει ο άρρωστος από το νόσημα Ν, όταν το αποτέλεσμα της δοκιμασίας είναι αρνητικό. Δεν πρέπει να συγχέεται με το αρνητικό διαγνωστικό σφάλμα, που εκφράζει την πιθανότητα να πάσχει από το νόσημα Ν, όταν το αποτέλεσμα είναι αρνητικό.

ΒΙΒΛΙΟΓΡΑΦΙΑ

  1. ΒΑΣΙΛΕΙΟΥ Δ. Διαγνωστική Mεθοδολογία και Διαφορική διαγνωστική. Κοβάνης Ιατρικά Βιβλία, Αθήνα, 1956
  2. ΣΠΑΡΟΣ Λ. Θεωρία της Λήψης των Κλινικών Αποφάσεων. Εκδόσεις Βήτα, Αθήνα, 1999
  3. ΜΙΕΤΤΙΝΕΝ ΟS. Advanced Study Design. The Erasmus Summer Programme, Rotterman, 1997
  4. ΜΙΕΤΤΙΝΕΝ ΟS, CARO JJ. Foundations of medical diagnosis: what actually are the parameters involved in Bayes theorem? Stat Med 1994, 13:201–209
  5. SOX HC, BLATT MA, HIGGINS MC, MARTON KI. Medical Decision Making. Butterworth, Heinemann, London, 1988
  6. FLETCHER RH, FLETCHER SW, WAGNER EH. Clinical Epidemiology. The essentials. 2nd ed. Williams and Wilkins, London, 1988
  7. WULFF HR, PEDERSEN SA, ROSENBERG R. Philosophy of Medicine. An introduction. Blackwell Scientific Publ, London, 1990
  8. GRENIER B. Evaluation de la Decision Medical. Masson, Paris, 1996

 

© 2000, Αρχεία Ελληνικής Ιατρικής