Τελ. ενημέρωση:
19-Sep-2000

Αρχ Ελλ Ιατρ, 16(5), Σεπτέμβριος-Οκτώβριος 1999, 511-515

ΕΦΑΡΜΟΣΜΕΝΗ ΙΑΤΡΙΚΗ ΕΡΕΥΝΑ

Εφαρμογή του μπαγιεσιανού διαγνωστικού διαλογισμού
σε ένα μη ιατρικό πρόβλημα*

Λ. ΣΠΑΡΟΣ
Εργαστήριο Κλινικής Επιδημιολογίας, Τμήμα Νοσηλευτικής, Πανεπιστήμιο Αθηνών

Λέξεις ευρετηρίου: Βάρος μαρτυρίας, Λόγος νέας πληροφορίας, Λότζιτ, Μπαγιεσιανός διαλογισμός, Οτζ.

1. ΕΙΣΑΓΩΓΗ

Η μπαγιεσιανή μέθοδος αποτελεί, μαζί με τη μέθοδο της λογιστικής παλινδρόμησης, τις δύο μεθόδους που χρησιμοποιούνται σήμερα για τον υπολογισμό της στατιστικής πιθανότητας ενός νοσήματος.¹ Η στατιστική αυτή πιθανότητα περιέχεται στις πιθανολογικές υποθέσεις, που αποτελούν τη βασική προκειμένη του λογικού σχήματος της στατιστικής εξήγησης ή, καλύτερα, της στατιστικής θεμελίωσης στο χώρο της διάγνωσης. Η διάγνωση, ως γνωστό, υπακούει στο λογικό σχήμα της στατιστικής (πιθανολογικής ή στοχαστικής) εξήγησης. Η μείζων προκειμένη του υποθετικού διαγνωστικού διαλογισμού έχει το χαρακτήρα δεσμευμένης πιθανότητας και συγκεκριμένα εκφράζει τη (στατιστική) πιθανότητα ενός νοσήματος Ν με δεδομένη μια ορισμένη κλινική εικόνα Ε: Pr (νόσημα Ν/κλινική εικόνα Ε). Ο υπολογισμός της πιθανότητας αυτής απαιτεί μελέτες εφαρμοσμένης έρευνας, οι οποίες σπανίζουν στη διεθνή βιβλιογραφία. Είναι σκόπιμο να τονισθεί ότι η στατιστική (διαγνωστική) εξήγηση μιας αρρώστιας δεν έχει τη γνωστική ισχύ της νομολογικής-παραγωγικής εξήγησης ή μάλλον δεν είναι γνήσια εξήγηση, αλλά απλώς θεμελιώνει την ορθολογική προσδοκία ότι ο άρρωστος πάσχει από το νόσημα Ν. Οι εκφράσεις «είναι πολύ πιθανό» ή «είναι σχεδόν βέβαιο» ή οι αντίστοιχες «πιθανότητες» δεν είναι στατιστικές αλλά «επαγωγικές» και δεν υπακούουν στα κριτήρια του Kolmogorov. Δεν αποτελούν ποσοδείκτες, αλλά εκφράζουν σχέσεις μεταξύ της στατιστικής υπόθεσης (ή στατιστικού νόμου) και των συνθηκών εφαρμογής του νόμου, δηλαδή του explanans αφενός και του συμπεράσματος (του explanandum) αφετέρου. Το explanandum (το εξηγητέο) στη διαγνωστική λογική αποτελεί την ατομική πρόταση, που περιγράφει ότι ο άρρωστος με την κλινική εικόνα Ε πάσχει με πιθανότητα Χ από το νόσημα Ν.²

Η μπαγιεσιανή προσέγγιση για τον υπολογισμό της διαγνωστικής πιθανότητας ενός Ν με βάση μια ορισμένη κλινική εικόνα Ε εισήχθη για πρώτη φορά στην Ιατρική το 1959 και έκτοτε έχει τύχει σχετικώς ευρείας εφαρμογής, ιδιαίτερα στον ομαδικό ή και τον προσυμπτωματικό έλεγχο αλλά και στην κλινική διάγνωση.³ Παρά την ευρεία χρησιμοποίησή του και την εισαγωγή του σε προγράμματα ηλεκτρονικών υπολογιστών, που βοηθούν στη διάγνωση ή κατανόησή του, συχνά συναντά δυσκολίες, ιδιαίτερα από έμπειρους γιατρούς, που ενίοτε φθάνουν να αρνούνται τη χρησιμότητά του.

Στο παράδειγμα που ακολουθεί, θα εφαρμοστεί ο μπαγιεσιανός διαλογισμός σε μια μη ιατρική περίπτωση, που θα βοηθήσει ενδεχομένως στην κατανόηση των δύο βασικών προαπαιτουμένων για τον υπολογισμό της «διαγνωστικής πιθανότητας». Το παράδειγμα με διάφορες παραλλαγές χρησιμοποιείται συχνά σε φροντιστηριακές ασκήσεις της κλινικής επιδημιολογίας διαφόρων ιατρικών σχολών του εξωτερικού και είναι γνωστό ως «το πρόβλημα του χρώματος του ταξί σ’ ένα τροχαίο δυστύχημα» (“traffic accident and taxi colour”).^4,5

2. ΠΑΡΑΔΕΙΓΜΑ

Κατά τη διάρκεια της νύκτας, ένας πεζός παρασύρεται από ένα ταξί, που τον εγκαταλείπει αβοήθητο. Ένας μάρτυρας καταθέτει ότι το ταξί ήταν χρώματος μπλε. Στην πόλη υπάρχουν δύο εταιρίες ταξί, η μια που διαθέτει ταξί χρώματος μπλε (που αποτελούν το 15% του συνολικού αριθμού ταξί, δηλαδή p=0,15) και η άλλη χρώματος πράσινου (που αποτελούν το 85%, δηλαδή 1–p=0,85). Για να ελεγχθεί η εγκυρότητα του μάρτυρα υποβάλλεται σε μια δοκιμασία: θα πρέπει δηλαδή να αναγνωρίσει, κατά τη διάρκεια της νύκτας, το χρώμα σ’ ένα σύνολο ταξί, από τα οποία τα μισά είναι χρώματος μπλε. Ο μάρτυρας υποβάλλεται στη δοκιμασία και αναγνωρίζει ορθά τα δύο χρώματα στο 80% των περιπτώσεων. Το πρόβλημα, του οποίου ζητείται η λύση, είναι να εκτιμηθεί η πιθανότητα ότι το ταξί που προκάλεσε το ατύχημα ήταν όντως μπλε, όπως ισχυρίζεται ο μάρτυρας. Το δικαστήριο αλλά και οι ασφαλιστικές εταιρίες θα θεωρήσουν υπεύθυνη την εταιρία ταξί, της οποίας η πιθανότητα ν’ ανήκει το ταξί σ’ αυτή είναι μεγαλύτερη του 0,50. Αντίθετα προς την ενορατική απάντηση, η πιθανότητα ότι ένα ταξί μπλε ευθύνεται για το ατύχημα δεν ισούται με 0,80. Επτά διαφορετικοί τρόποι εφαρμογής του μπαγιεσιανού διαλογισμού έχουν προταθεί για τη λύση του προβλήματος.

1η λύση: Μέθοδος του τετράπτυχου πίνακα

Αποτελεί τον απλούστερο τρόπο λύσης του προβλήματος. Στον πίνακα 1 φαίνονται οι αληθώς (12) και ψευδώς (17) θετικές απαντήσεις (ότι το ταξί ήταν μπλε) του αυτόπτη μάρτυρα του δυστυχήματος, που υποβλήθηκε στη δοκιμασία κατά τη διάρκεια της νύκτας.

Καταρχήν, η a priori (ή πρωτογενής) πιθανότητα να ήταν ένα ταξί χρώματος μπλε υπεύθυνο του ατυχήματος ισούται με p=0,15 και χρώματος πράσινου (1–p)= 0,85, ενώ η πιθανότητα να είναι μπλε το ταξί που προκάλεσε το ατύχημα, εάν ο μάρτυρας καταθέσει ότι ήταν μπλε, ισούται με 12/29=0,41. Η κατάθεση του μάρτυρα αύξησε, δηλαδή, την πιθανότητα από 0,15 σε 0,41, πιθανότητα όμως που εξακολουθεί να είναι μικρότερη από 0,50. Και επομένως, η πιθανότητα ένα ταξί πράσινο να προκάλεσε το ατύχημα εξακολουθεί να είναι μεγαλύτερη και ίση προς 0,59. Από τον πίνακα προκύπτει ότι, εάν ο μάρτυρας καταθέσει ότι το ταξί ήταν πράσινο, τότε η πιθανότητα από 0,85 μετατρέπεται σε 0,96, ενώ η πιθανότητα το ταξί να ήταν μπλε καθίσταται αμελητέα (0,04). Η ασυμμετρία αυτή των «δευτερογενών πιθανοτήτων»* (ΔΠ), παρά την ικανότητα του μάρτυρα να αναγνωρίζει ορθά εξίσου τα μπλε (0,80) και τα πράσινα αυτοκίνητα (0,80), οφείλεται στο διαφορετικό ποσοστό μπλε και πράσινων ταξί στην πόλη όπου έγινε το ατύχημα.^5,6

2η λύση: Εφαρμογή του κλασικού τύπου του θεωρήματος του Bayes

Υπενθυμίζεται πως το ερώτημα που τίθεται είναι: «ποια είναι η πιθανότητα το ταξί που προκάλεσε το ατύχημα να είναι χρώματος μπλε, με δεδομένο ότι ο μάρτυρας κατέθεσε ότι ήταν μπλε;».

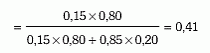
3η λύση: Ο τρόπος αυτός συνίσταται απλώς στη μεταφορά σε πίνακα των δεδομένων του προηγουμένου τύπου

Στον πίνακα 2 φαίνονται τα ποσοστά των ταξί διαφορετικού χρώματος στην πόλη όπου έγινε το ατύχημα, το ποσοστό των αληθώς και ψευδώς θετικών απαντήσεων του μάρτυρα, καθώς και οι δευτερογενείς πιθανότητες.^7,8

4η λύση: Χρησιμοποίηση των λόγων πιθανοφάνειας*

Η πιθανότητα της απάντησης του μάρτυρα ότι «το ταξί ήταν χρώματος μπλε», όταν όντως αυτό ήταν μπλε, είναι 0,80 (ποσοστό αληθώς θετικών απαντήσεων) και η πιθανότητα της απάντησης «χρώματος μπλε», όταν το ταξί ήταν στην πραγματικότητα πράσινο, είναι 0,20 (ποσοστό ψευδώς θετικών απαντήσεων). Ο θετικός λόγος πιθανοφάνειας, επομένως, ισούται με L=0,80/0,20=4 και ο αρνητικός λόγος πιθανοφάνειας με λ=0,20/0,80=0,25. Σύμφωνα με το συνήθη τύπο του θεωρήματος του Bayes, η δευτερογενής πιθανότητα (ΔΠ) ισούται με:

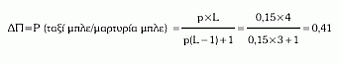
Εάν ο μάρτυρας, αντίθετα, καταθέσει ότι το υπεύθυνο ταξί ήταν χρώματος πράσινου, τότε η πιθανότητα το υπεύθυνο του ατυχήματος ταξί να ήταν στην πραγματικότητα μπλε ισούται με:

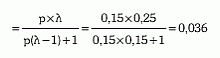
Το «διάστημα ασφαλείας» της κατάθεσης του μάρτυρα περιλαμβάνεται μεταξύ p₁ και p₂, όπου:

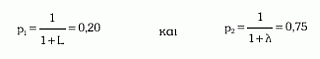
Όταν, δηλαδή, ο επιπολασμός των μπλε ταξί κυμαίνεται μεταξύ 0 και 0,20, τότε οποιαδήποτε και αν είναι η κατάθεση του μάρτυρα για το χρώμα του ταξί, η δευτερογενής πιθανότητα του μπλε ταξί θα είναι μικρότερη από 0,50, δηλαδή μικρότερη εκείνης των πράσινων ταξί (0,59).^4,9

5η λύση: Πιθανότητες σε οτζ (odds)

Το οτζ του επιπολασμού των μπλε ταξί ισούται με 0,15/0,85=Ω=0,176 και το οτζ της δευτερογενούς πιθανότητας με Ω΄L=0,176΄4=0,70 και άρα η δευτερογενής (εκ των υστέρων) πιθανότητα (ΔΠ) ισούται με:

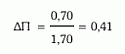
6η λύση: Νεπέρειος λογάριθμος των οτζ

Υπενθυμίζεται ότι ο λογάριθμος του οτζ (odds) φέρεται ως λότζιτ (logit).¹⁰ Ο επιπολασμός των μπλε ταξί (0,15) μετατρέπεται σε λότζιτ του 0,15 ως εξής:

ln (οτζ του 0,15)=ln 0,176=100 ln Ω=–1,73

Η πληροφοριακή αξία (ή το βάρος μαρτυρίας) της κατάθεσης του μάρτυρα ότι το ταξί ήταν μπλε, ισούται με:

ln L=ln 4=1,386 ή, καλύτερα, το σκορ της πληροφοριακής αξίας ισούται με: 100 ln 4=138,6* και άρα η δευτερογενής (μετά τη μαρτυρία) πιθανότητα (ΔΠ), εκφρασμένη σε λότζιτ, ισούται με:

100 ln (οτζ ΔΠ)=100 ln Ω+100 ln L=(–173)+138,6=(–34)

το οτζ της ΔΠ=e^-0,34=0,71 και, τέλος, η δευτερογενής πιθανότητα ισούται με:

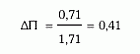
7η λύση: Δένδρο πιθανότητας

Η πιθανότητα της ένωσης «ποσοστό ταξί μπλε» (0,15) και «απάντηση ταξί μπλε» (0,80) ισούται με 0,15 x0,80=0,12. Η πιθανότητα της ένωσης «ποσοστό των πράσινων ταξί» (0,85) και της απάντησης «ταξί μπλε» (0,20) ισούται με 0,85 x 0,20=0,17. Οι δύο αυτές πιθανότητες μεταφέρονται στο δένδρο απόφασης και το άθροισμά τους ισούται με 0,12+0,17=0,29 (εικόνα 1).^8,9

Στο δένδρο, ο κλάδος «ταξί μπλε», που καταλήγει στην πιθανότητα 0,12, έχει πιθανότητα (p) τέτοια, ώστε 0,29x (p)=0,12 και άρα:

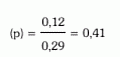
είναι η πιθανότητα να είναι υπεύθυνο ένα ταξί μπλε, εάν ο μάρτυρας καταθέσει ότι το ταξί ήταν χρώματος μπλε.

Ο κλάδος «ταξί πράσινο», που καταλήγει στην πιθανότητα 0,17, έχει πιθανότητα (p) ίση με 0,59. Είναι η πιθανότητα να είναι υπεύθυνο ένα «ταξί πράσινο», ενώ ο μάρτυρας έχει καταθέσει ότι ήταν χρώματος μπλε.

Το άθροισμα των πιθανοτήτων (0,12)+(0,17)=(0,29) είναι η πιθανότητα της απάντησης του μάρτυρα «ταξί μπλε» στον πληθυσμό των ταξί που υποβλήθηκε σε έλεγχο. Δηλαδή, ο μάρτυρας σε ένα σύνολο 100 ταξί (15 μπλε και 85 πράσινα) θα κατέθετε ότι υπάρχουν 29 μπλε και 71 πράσινα.

Ο λόγος φέρεται ως «λόγος της νέας πληροφορίας», που θα τροποποιήσει την πρωτογενή (χωρίς μάρτυρα) πιθανότητα των μπλε ταξί.

P (μπλε ταξί/κατάθεση «μπλε ταξί»)=επιπολασμός x λόγος νέας πληροφορίας=0,15 x 2,76=0,41.

Υπό το φως της νέας πληροφορίας, που παρέχεται από το μάρτυρα, η νέα εκτίμηση της πιθανότητας της υποτιθέμενης «αιτίας του ατυχήματος» θα θεμελιώσει την απόφαση που θα ληφθεί από τις αρχές ή τους δικαστές. Όταν λείπουν μαρτυρίες, τότε η κρίση θα βασιστεί μόνο στον επιπολασμό και θα ενοχοποιηθεί η εταιρία που διαθέτει τα περισσότερα ταξί, δηλαδή τα πράσινα. Εντούτοις, παρά την ύπαρξη της μαρτυρίας, η πιθανότητα το υπεύθυνο του ατυχήματος ταξί να είναι χρώματος μπλε παραμένει μικρότερη του 0,50. Οι ειδικοί θα πρέπει να κρίνουν αν η πιθανότητα αυτή είναι επαρκής ή όχι, για να δικαιολογήσει την απόφαση, την οποία πιστεύουν ότι είναι ορθό να πάρουν.

Είναι ενδιαφέρον να υπολογιστεί ποια θα πρέπει να είναι η ικανότητα του μάρτυρα να διακρίνει τη νύκτα τα δύο χρώματα των ταξί, που θα έδινε στην τελική πιθανότητα ότι το ταξί ήταν μπλε τιμή μεγαλύτερη από 0,50. Σύμφωνα με τα δεδομένα του δένδρου, η πιθανότητα αυτή μπορεί να υπολογιστεί με τον τύπο:

άρα: p>=0,85

Αρκεί, δηλαδή, η διακριτική ικανότητα του μάρτυρα να υπερβαίνει κατά 0,05 μόνο την παρατηρηθείσα τιμή (0,80), για να αναστραφεί η τελική κρίση.

Για να μην υπερβαίνει το ανώτερο όριο του «διαστήματος εμπιστοσύνης» της παρατηρηθείσας τιμής (0,80) την τιμή 0,85, θα έπρεπε η μέτρηση να είχε γίνει σε δύο ομάδες με αριθμό ταξί (η) τέτοιον, ώστε να ισχύει ο τύπος:

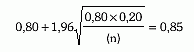
ώστε (n)=250 ταξί σε κάθε ομάδα.

Η ανάλυση αυτή, γνωστή και ως ανάλυση ευαισθησίας, μετράει την ευαισθησία της κρίσης σε συνάρτηση με τη μεταβλητότητα ενός τυχαίου παράγοντα. Η ανάλυση δείχνει, προφανώς, ότι η τελική κρίση δεν μπορεί να βασιστεί μόνο στην κατάθεση του μάρτυρα και ότι απαιτείται η αναζήτηση συμπληρωματικής πληροφορίας.

3. ΣΥΜΠΕΡΑΣΜΑ

Το παράδειγμα που αναπτύχθηκε, δείχνει τη δυνατότητα εφαρμογής του μπαγιεσιανού διαλογισμού σ’ ένα πρακτικό μη ιατρικό πρόβλημα και συγχρόνως την αναλογία του παραδείγματος με τη διαγνωστική λογική. Τα ποσοστά των «μπλε» και «πράσινων ταξί» αντιστοιχούν στις πιθανότητες (επιπολασμό) του αναζητούμενου νοσήματος και των διαφοροδιαγνωστικώς συναφών νοσημάτων (πρωτογενείς πιθανότητες). Η κατάθεση του μάρτυρα για τα ποσοστά των μπλε και πράσινων ταξί, κατά τη δοκιμασία που υποβλήθηκε κατά τη διάρκεια της νύκτας, αντιστοιχούν στις διαγνωστικές ποιότητες ή πιθανοφάνειες της κλινικής εικόνας με δεδομένο το νόσημα και τα διαφοροδιαγνωστικώς συναφή νοσήματα. Τέλος, η τελική κρίση για το χρώμα του ταξί, που προκάλεσε το ατύχημα, αντιστοιχεί στη δευτερογενή διαγνωστική πιθανότητα ή προβλεπτική αξία.

ΒΙΒΛΙΟΓΡΑΦΙΑ

1. MIETTINEN OS. Advanced study design. The Erasmus Summer Programme, Rotterdam, 1997
2. ΓΕΜΤΟΣ Π. Μεθοδολογία των κοινωνικών επιστημών. Γ’ έκδοση. Εκδόσεις Παπαζήση, Αθήνα, 1987
3. LEDLEY RS, LUSTED LB. Reasoning foundations of medical diagnosis. Science 1959, 130:9–21
4. GRENIER B. Evaluation de la decision medicale. Introduction a l’analyse medico-economique. Masson, Paris, 1996
5. SACKETT DL, HAYNES RB, GUYATT GH, TUGWELL P. Clinical Epidemiology. A basic science for clinical medicine. 2nd ed. Little, Brown and Co, London, 1991:3–69
6. WULFF H. Rational diagnosis and treatment: an introduction to clinical decision-making. Blackwell, Oxford, 1981
7. FLETCHER RH, FLETCHER SW, WAGNER EH. Clinical Epidemiology. The essentials. 2nd ed. Williams and Wilkins, London, 1988
8. SOX HC, BLATT MA, HIGGINS MC, MARTON KI. Medical decision making. Butterworth-Heinemann, London, 1988:102
9. ΣΠΑΡΟΣ Λ. Θεωρία της λήψης των κλινικών αποφάσεων. Εκδόσεις Βήτα, Αθήνα, 1999
10. McCARTNEY FJ. Diagnostic logic. In: Phillips CI (ed) Logic in Medicine. BMG, London, 1989:33–58
11. SPIEGELHALTER DJ, KNILL-JONES RP. Statistical and knowledge based approaches to clinical-support systems with an application to gastroenterology. J Roy Stat Soc 1984, 147:37–77